안녕하세요 Dibrary입니다.
이번 시간에는 파이썬으로 Anderson-Darling 통계량을 확인해 보는 방법을 소개하겠습니다.
먼저, Anderson-Darling 통계를 보기전에, 먼저 알아야 할 사전 지식은 3가지가 있습니다.
- 귀무가설
- 대립가설
- P-value
통계를 공부 해 보신 분이라면 당연히 알 수 있겠지만, 모르는 분들을 위해 간략히 소개만 해 보겠습니다.
| 귀무가설(H0) | 쉽게 표현하자면 '차이가 없다'라고 주장하는 가설이라고 보시면 됩니다. 그리고, 이 가설이 맞지 않음을 즉, '차이가 있음'을 통계학적 증거로 증명하면 됩니다. |
| 대립가설(H1) | 귀무가설의 반대입니다. '차이가 있다' 라고 보통 주장하는 가설입니다. 귀무가설의 기각 여부가 대립가설의 통계학적 결과로 판별 됩니다. |
| P-value | 관측된 데이터가 귀무가설과 양립하는 정도를 0~1 사이의 수치로 표현한 값입니다. P-value 값이 낮을수록 그 정도가 약하다고 보며, 기준값(0.05나 0.01)보다 낮을 경우 귀무가설을 기각합니다. |
복잡하면 그냥 간단하게만 생각하세요.
귀무가설 = 기각하고자 하는 가설
대립가설 = 증명하고자 하는 내용
아무래도 통계 용어다 보니까 어려우실 수도 있습니다. 중요한 것은 위의 내용이 정의되어 있지만, '그런게 있구나~' 하고 넘어가셔도 됩니다.
이제 본격적으로 Anderson-Darling 통계를 보죠.
Anderson-Darling 통계는 데이터가 특정분포를 얼마나 잘 따르는지를 확인하고 싶을 때 사용합니다.
대개 데이터의 갯수가 5000개 미만일 경우에는 Shapiro-Wilk 검정을 하고, 그 보다 갯수가 많으면 Anderson-Darling 통계를 사용합니다.
여기서 '특정분포'란 대부분 정규분포인 경우가 많습니다.
실 사례를 소개해보자면, 저는 프로그램으로 수집한 데이터들이 T-test를 하기 전에 정규성을 만족하는지 사전에 데이터를 체크하는 용도로 사용했었습니다. (물론, 평균적으로 비교하는 데이터의 갯수는 많지 않았습니다만, 특별한 경우에 데이터가 많은 순간이 있어서 AD를 사용했습니다.)
Anderson-Darling 통계의 귀무가설과 대립가설은 아래와 같습니다.
| 귀무가설 | 데이터가 특정 분포를 따른다. |
| 대립가설 | 데이터가 특정 분포를 따르지 않는다. |
만약 통계 결과가 대립가설이 맞는 것으로 나온다면? 귀무가설을 기각하게 되겠네요.
먼저 Anderson-Darling 통계를 사용하려면 scipy 모듈을 설치 해야 합니다.
Jupyter를 실행 한 후에, 터미널에서 pip install scipy를 입력하시면 자동으로 설치 됩니다. 저는 미리 설치가 되어 있었어서 아래와 같이 already satisfied 라는 문구가 나오네요.

설치를 완료 하셨으면, import scipy.stats 를 하시면 됩니다. 이는 scipy 안에 있는 통계 모듈을 사용하기 위한 것이죠.
제가 임의로 데이터를 하나 만들고, 해당 데이터의 분포를 matplotlib을 이용해서 시각적으로 보여드리겠습니다.
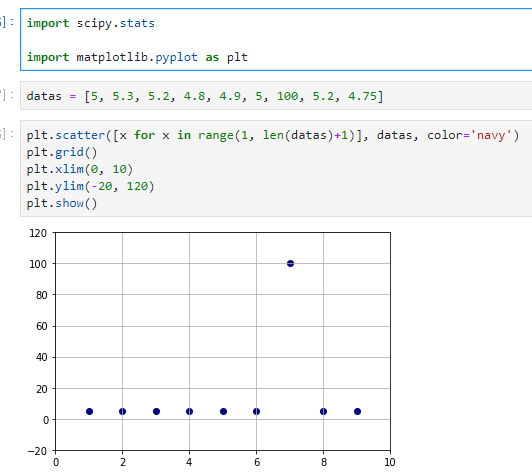
우선 임의 데이터는 datas라는 변수로 담았습니다.
아래 차트로 그렸는데, 잘 보시면 100이라는 하나의 값만 약 5 근처의 값으로부터 많이 떨어져 있죠?
그러면 이제 Anderson-Darling 통계값 확인을 해 보겠습니다. 그냥 데이터를 anderson 함수에 넣어 주시면 됩니다. 엄청 쉽죠?

네 저는 anderson함수의 결과를 AD_value라는 변수로 받았고, 해당 결과는 위와 같이 나옵니다. 그 중에 첫 번째 값만 뽑아내어서 확인해보니 2.767이 나옵니다.
먼저 값을 설명 해 드리면, 첫 번째 값은 검정통계량입니다. 그리고 그 뒤에 critical_values는 임계값들이죠.
significance_level은 알파값(α) 입니다.
알파는 유의수준이라고도 하며, 귀무가설이 참인데도 기각할 확률을 의미합니다. 즉, 알파 수준을 높게 잡으면 잘못 판단할 위험성을 더 높게 설정한다는 것과 같습니다.
알파 값은 총 5개가 있는데, 각각 [0.15, 0.1, 0.05, 0.025, 0.01] 이 됩니다.
그러면 알파 값에 해당되는 임계값이 또 매치가 되죠? 0.01알파값의 임계값은 0.961입니다.
이제 정규성을 만족하는지는 어떻게 확인하느냐면, 뒤의 critical_values와 significance_level을 비교해서 확인할 수 있습니다.
해석은 아래와 같이 합니다.
- 알파값 0.01에 대해서 임계값은 0.961이고, 검정통계량이 2.767이므로, 이는 검정통계량보다 임계값이 작으므로 결과는 유의수준(알파값) 0.01에서 유의합니다.
- 알파값 0.025에 대한 임계값은 0.808이고, 검정통계량이 2.767이므로, 이는 검정통계량보다 임계값이 작으므로 결과는 유의수준(알파값) 0.025에서 유의합니다.
나머지들도 위와 같이 비교해보면 되는데 위 값은 모두 2.767보다 작으므로, 선택한 유의수준(알파값)과 관계없이 귀무가설을 기각합니다.
귀무가설을 기각한다는 것은? 데이터가 특정 분포(정규분포)를 따르지 않는다는 것이 됩니다.
그러면 임의로 넣은 데이터를 다르게 바꿔보겠습니다.

아까와는 다르게 5 부근의 값들로만 구성을 해 보았습니다.
검정 통계량은 0.116이고, 딱 봐도 검정통계량 값이 모든 critical_values보다 작죠?
즉, 5개의 어느 알파값에 대해서든지, 검정통계량이 임계값보다 작으므로 귀무가설을 기각하지 않습니다.
귀무가설을 기각하지 않는다는 것은 "데이터가 특정 분포를 따른다" 가 됩니다.
'프로그래밍 > Python' 카테고리의 다른 글
| 파이썬 데이터 분석 준비! - Numpy배열 다루기 - 2(배열 데이터 다루기) (0) | 2022.03.24 |
|---|---|
| Dixon Q test - 특이치 식별 및 제거, 파이썬으로 구현 (0) | 2022.03.23 |
| 파이썬 데이터 분석 준비! - Numpy배열 다루기 - 1(객체 만들어보기) (0) | 2022.03.15 |
| 알고리즘을 풀 때 항상 생각해봐야 하는 것 - 복잡도 (0) | 2022.02.16 |
| 파이썬으로 구현해 확인하는 OPCUA통신 - Server편 (15) | 2022.02.09 |